Support Vector Machine: A Complete Overview Of SVM Classification

How can your business leverage a support vector machine to unlock data insights and make more accurate decisions? As one of the most powerful algorithms in machine learning, the support vector machine provides effective solutions for classification, regression, and pattern recognition. In this guide, MOR Software will explore in detail how it works and how to identify the most suitable applications for your business.

What Is Support Vector Machine?

Support vector machine (SVM) is a powerful algorithm in machine learning, used for classifying data and predicting accurate outcomes. It works by identifying important support vectors, which determine the optimal hyperplane to separate different data classes.

The support vector machine was first developed by Vladimir Vapnik and his colleagues at Bell Labs in the 1990s. This was a breakthrough in machine learning support vector machines, aiming to build a vector machine classifier capable of highly accurate data classification.

The original concept was based on statistical learning theory, introduced by Vapnik, focusing on finding the optimal hyperplane to separate data classes. The creation of the support vector machine model marked a new era for machine learning SVM, widely applied in both research and practical projects.

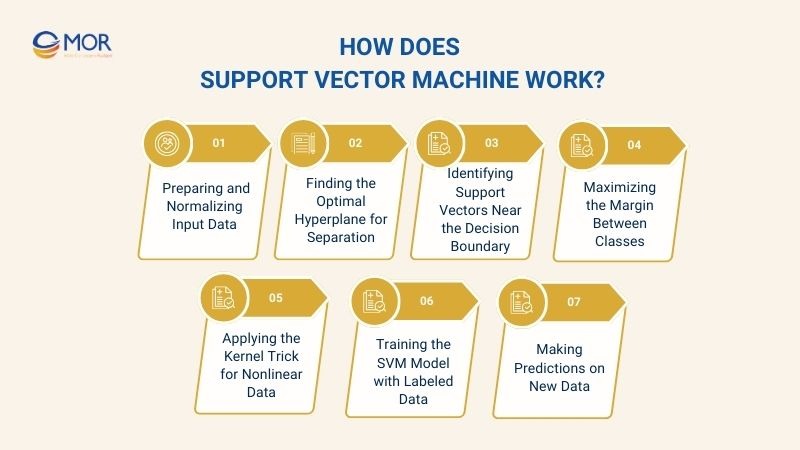
How Does Support Vector Machine Work?

Support vector machines (SVMs) in machine learning are powerful algorithms used for accurate data classification and prediction. Below is how a support vector machine model works.

Step 1 – Preparing and Normalizing Input Data

Before building a support vector machine model, the first crucial step is to prepare the input data. The data must be cleaned, removing missing or anomalous values, to ensure that machine learning support vector machines operate effectively.

Next, the data should be normalized or scaled to the same range to prevent features with large values from dominating the classification process. This normalization helps vector machine classifiers learn more accurately and identify the optimal hyperplane for support vector machine classification.

Step 2 – Finding the Optimal Hyperplane for Separation

After normalizing the input data, the next step in the support vector machine learning model is to find the optimal hyperplane to separate different data classes. A hyperplane is a plane (or hypersurface) in multi-dimensional space that separates points from different classes while maximizing the margin between them.

Step 3 – Identifying Support Vectors Near the Decision Boundary

Once the optimal hyperplane is determined, the support vector machine focuses on the most critical data points – the support vectors. These are points near the decision boundary that directly influence the hyperplane's position.

In a support vector machine model, accurately identifying support vectors optimizes classification performance and reduces errors. Data points that are not support vectors do not affect the decision boundary, ensuring the machine learning support vector machines remain stable and highly accurate.

Step 4 – Maximizing the Margin Between Classes

A key principle of support vector machine learning is to maximize the margin—the distance between the hyperplane and the support vectors of each class. A larger margin reduces misclassification on new data and enhances the model's generalization ability.

In a vector machine classifier, maximizing the margin is crucial for building an effective support vector machine model, especially when handling noisy or unevenly distributed data.

Step 5 – Applying the Kernel Trick for Nonlinear Data

When the data cannot be separated by a linear hyperplane, machine learning SVM uses the kernel trick to map the data into a higher-dimensional space. This transformation makes nonlinear data linearly separable, allowing the support vector machine model to identify the optimal hyperplane.

Step 6 – Training the SVM Model with Labeled Data

Next, the support vector machine is trained using labeled data. In this step, the machine learning algorithm optimizes the hyperplane based on support vectors and the chosen kernel functions.

Training allows the support vector machine model to learn the relationship between data features and labels, enabling accurate classification of new data. Machine learning support vector machines are known for strong generalization, even when trained on small or high-dimensional datasets.

Step 7 – Making Predictions on New Data

After training, the support vector machine model can predict labels for new, unseen data. The model determines the class by analyzing the position of new data points relative to the hyperplane and support vectors.

Thanks to prior optimization, support vector machine learning ensures stable and precise predictions. Vector machine classifiers are widely applied in image classification, text recognition, and many other predictive tasks within machine learning.

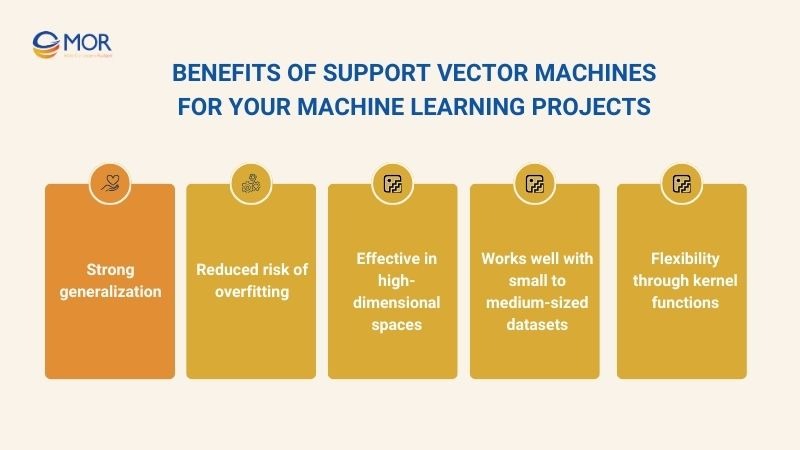
Benefits Of Support Vector Machines For Your Machine Learning Projects

Support vector machine brings significant benefits to machine learning projects. Here are the key advantages of using a support vector machine model.

Strong generalization

One of the standout advantages of the support vector machine model is its strong generalization capability. By maximizing the margin between data classes, machine learning support vector machines can make accurate predictions on unseen data.

According to an experimental study, applying support vector machine classification on the Iris dataset achieved an accuracy of up to 97.78% on the test set.

Reduced risk of overfitting

Another significant benefit of the support vector machine model is its reduced risk of overfitting. This is due to the mechanism of maximizing margins and relying only on crucial support vectors. 

In machine learning support vector machines, focusing on data points near the decision boundary helps the vector machine classifier avoid being overly influenced by noise or atypical data.

Effective in high-dimensional spaces

The support vector machine model is particularly effective when working with high-dimensional data. Using the kernel trick, machine learning support vector machines can map nonlinear data to a higher-dimensional space. 

This allows the support vector machine model to easily identify the optimal hyperplane.

Works well with small to medium-sized datasets

Unlike many other algorithms, the support vector machine model does not require massive datasets to perform well. Machine learning support vector machines can still deliver strong results even with small to medium-sized datasets by learning from the most critical support vectors.

A study analyzing the performance of big data machine learning models on 18 small medical datasets found that SVM was among the most powerful algorithms when handling small datasets, demonstrating its strong generalization capabilities (source).

Flexibility through kernel functions

Another strength of the support vector machine model is its flexibility through kernel functions. Machine learning support vector machines can use linear, RBF, polynomial, or sigmoid kernels to handle nonlinear data.

This allows the vector machine classifier to adapt to various data types while maintaining the high effectiveness of support vector machine classification.

Popular Types Of Support Vector Machine Classification

In machine learning, there are various types of support vector machine models used depending on the nature of the data and the classification objectives. Here are three popular types.

Linear Support Vector Machines

Linear support vector machines are a type of support vector machine model used when data can be separated linearly. This means different data classes can be divided by a straight line (hyperplane) in the feature space.

In machine learning, Linear SVM learns from support vectors to determine the optimal decision boundary while maximizing the margin between classes.

Practical applications of linear support vector machines include:

• Email spam classification
• Handwritten digit recognition using the MNIST dataset
• Credit risk prediction in finance

Example: Suppose you have a dataset of handwritten digits from 0 to 9 (like MNIST) and want a computer to classify each digit correctly. Linear support vector machines will:

• Learn from the most important images (support vectors) to draw a “dividing line” between different digits.
• When encountering new images, the model uses these support vectors to predict the correct digit, achieving around 92–95% accuracy.

This demonstrates the effectiveness of support vector machine models when data can be separated by a straight line.

Nonlinear Support Vector Machines

Nonlinear support vector machines are a type of support vector machine model used when data cannot be separated by a straight line (hyperplane). In machine learning, a nonlinear SVM uses the kernel trick to map nonlinear data into a higher-dimensional space. This allows the model to determine the optimal decision boundary even for complex datasets.

Practical applications:

• Facial recognition, where facial features have nonlinear relationships
• Medical image classification, such as distinguishing between benign and malignant tumors
• Predicting user behavior on websites based on diverse nonlinear interactions

Example: Suppose you want to classify different types of flowers based on features like petal length, petal width, and color. The data cannot be separated by a straight line. Nonlinear SVM will:

• Use a kernel function (e.g., RBF) to map data into a higher-dimensional space
• Find the optimal hyperplane in the new space to classify flower types accurately, achieving higher accuracy than Linear SVM

Support Vector Regression (SVR)

Support Vector Regression (SVR) is a variant of support vector machine models used for predicting continuous values rather than classification. SVR still relies on support vectors to optimize a “regression line,” minimizing the error between predicted and actual values within a defined range (epsilon margin).

Practical applications:

• Stock or currency price forecasting in finance
• Predicting electricity demand based on historical usage and weather data
• Estimating air pollution levels from environmental indicators

Example: Suppose you want to predict house prices based on area, number of rooms, and location. The data is continuous and nonlinear. SVR will:

• Learn from the most important support vectors to construct an accurate “regression line”
• Predict the approximate price of a new house, reducing error and aligning predictions with real-world data

>>> READ MORE: TOP 6 Information Sets Used in Machine Learning You Should Know

Mathematical Computation Of Support Vector Machines

In machine learning, understanding the mathematical computation of support vector machines is the foundation for building accurate support vector machine models. Here are the key aspects to grasp:

Linear Hyperplane Equation

In machine learning support vector machines, a linear hyperplane is a flat surface that separates data classes in the feature space. The general equation of a linear hyperplane is:

Significance: Every point at x on the hyperplane satisfies this equation. In a support vector machine model, the data points near the decision boundary (support vectors) help determine the optimal linear hyperplane, ensuring that the machine learning support vector machines classify data accurately.

Practical example: Suppose you want to separate two types of flowers based on petal length and width. The linear hyperplane calculated from support vectors divides the two classes, allowing the SVM to predict the type of a new flower correctly.

Linear SVM Classifier

In machine learning, the linear SVM classifier uses a linear hyperplane to separate data into classes. The classification rule is:

Practical example: Suppose you want to classify emails as spam or not spam. The linear support vector machines will:

• Learn from the most important emails (support vectors) to determine the decision boundary between spam and non-spam.
• When a new email appears, the model uses these support vectors to classify it accurately.

Significance: The linear SVM classifier maximizes the margin using support vectors, improving prediction accuracy and generalization for unseen data.

Optimization Problem in SVM

The goal is to find the optimal linear hyperplane by maximizing the margin:

Practical example: In the MNIST handwritten digits dataset, SVM optimizes the margin between digit “3” and “8” to predict new digits accurately.

Significance: The optimization problem in SVM ensures the support vector machine model classifies correctly while maintaining a wide margin, reducing the risk of overfitting, especially with noisy data.

SVM with Soft Margin

Soft margin allows some points to violate the margin, making SVM robust to noisy data:

Practical example: When predicting credit risk, some applications may contain unusual or noisy data. The soft margin allows the SVM to still find the optimal decision boundary.

Significance: SVM with soft margin increases the flexibility of the support vector machine model, ensuring high performance even with noisy or non-linear data.

Dual Problem in SVM

The dual problem in SVM simplifies optimization and enables the use of kernels:

Practical example: In face recognition, non-linear data points are mapped to a higher-dimensional space using a kernel. Only the key faces (support vectors) determine the decision boundary in this space.

Significance: The dual problem in SVM allows the support vector machine model to handle non-linear data efficiently using the kernel trick, while reducing computational complexity.

Decision Boundary in SVM

The decision boundary in SVM is determined by support vectors:

Practical example: In classifying Iris flowers, the decision boundary separates different flower types based on petal length and width. The points closest to the boundary (support vectors) determine its precise position.

Significance: The decision boundary in SVM enables the support vector machine model to classify accurately, maximize the margin, improve generalization, and reduce overfitting risk.

Drawbacks Of Support Vector Machines To Consider Before Implementation

Although the support vector machine model offers numerous advantages, there are still some limitations to consider before implementation. Here are the key points to keep in mind:

High computational cost on large datasets

A significant limitation of the support vector machine model is the high computational cost when working with large datasets. Training an SVM involves solving a quadratic optimization problem, requiring the computation of a kernel matrix with size proportional to the number of samples in the dataset.

As the number of samples increases, the required memory and computation time grow exponentially, making model training slow and resource-intensive. For example, with 30,000 samples, the number of operations can reach trillions, resulting in prolonged training time and practical challenges for deployment.

Sensitivity to feature scaling

In machine learning, the support vector machine model is highly sensitive to differences in scale and units of features. If features have different ranges, larger-valued features can dominate the decision boundary, lowering the model’s accuracy.

Therefore, feature scaling is crucial before training machine learning support vector machines, especially with RBF or polynomial kernels.. Ignoring this step can decrease support vector machine classification accuracy and compromise the model’s generalization performance.

Difficulty in selecting the kernel and hyperparameters

The kernel determines how the data is mapped to a higher-dimensional space, directly affecting the decision boundary and classification performance. Additionally, hyperparameters such as C (regularization) and gamma (in RBF kernel) require careful adjustment. 

Selecting the wrong kernel or hyperparameters not only reduces accuracy but may also lead to overfitting or underfitting.

Performance issues with overlapping data

The support vector machine model can struggle with datasets containing noise or overlapping classes. Since SVM relies on support vectors near the decision boundary, noisy points or outliers can distort it and lower accuracy.

Although soft margin can mitigate the impact of noise, performance may still lag compared to other models in highly cluttered datasets. A recent study proposed a modified SVM that replaces the slack variable with a binary variable to reduce noise influence, resulting in higher accuracy than traditional SVM on noisy datasets.

In Conclusion

The application of a support vector machine can transform the way your business processes data, recognizes patterns, and makes strategic decisions. In today’s competitive environment, integrating proven machine learning models has become essential. Contact MOR Software to implement customized support vector machine solutions that deliver efficiency, accuracy, and sustainable growth.